Flexoeffect in nematics
Flexoelectricity denotes curvature-induced electric polarisation in liquid
crystals, subjected to orientational deformations of the director field
1,2,3
(Figure 1).
. 
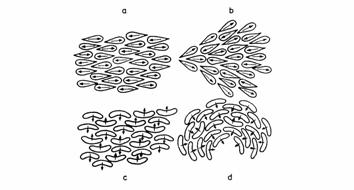Figure 1. The dipolar model of R. B. Meyer:
splay (a,b) and bend (c,d) deformation and corresponding polarization
Two
of the three basic modes (splay, bend and twist) posses the symmetry of a polar
vector. They are the splay: 
and
bend 
.
Thus, these deformations can polarize the initially centrosymmetric structure of
the nematic (Figure 1) according to the Curie principle4:
(1)
where the
coefficients e1z and e3x are the
flexoelectric coefficients of splay and bend in Meyer’s notation.
Flexocoefficients are measured in C/m (in SI system) and an order of magnitude
estimation yield e (electron charge)/(molecular lenght) = 4·10-11 C/m.
In the literature, however, usually one measures the flexocoefficients in c.g.s.
or dyn1/2. Equation (1) is the constitutive equation of the direct
flexoelectric effect. Experimental studies of this direct effect in nematics are
scarce. Experiments mostly deal with the converse flexoelectric effect: the
appearance of torques and orientational deformations in the director field
due
to external electric fields E(r). In this case the bulk
flexoelectric torque can be written in the form
,
where 
is
the bulk flexoelectric component of the molecular field5,6:
(2)
This expression can be transformed into an equivalent form:
(3)
The exact form of
this equation7 shows that the bulk
flexodeformations can be observed when there is a gradient in the distribution
of either the nematic director or an external electric field
,
or both. Effects of the first kind are known as linear (with respect to the
electric field) and they depend on the difference of splay and bend
flexocoefficients. Those of the second kind are known as gradient effects, and
they depend on the sum of both flexocoefficients (this is the total
flexocoefficient). It can be easily shown that for planar problems, where the
director field is confined to a plane, the first term in Eqn (3) is identically
zero. In such a case, with a homogeneous field, the only source of
flexodeformation comes from the surface torque at the liquid crystal/substrate
interface, 
,
where 
is
the flexoelectric surface molecular field6:
(4)
where
is
the surface normal. A complete solution of a static flexoelectric problem
requires the inclusion of the other torques in the torque balance equation, such
as elastic and dielectric ones in the bulk, and elastic, surface anchoring and
surface polarization ones at the surface2,6,8.
In the dynamic case viscous torques are also included, again bulk and surface
ones3.
Flexoeffect in a gradient electric field
The achievements of our group in the early study of the flexoeffects are connected with the discovery and study of the so-called gradient flexoelectric effect. There are three requirements for the observation of this effect: weak anchoring of the liquid crystal, at least at one of the two boundaries; existence of initial tilt of the director and finally, a non-homogeneity of the electric field. The combination of these three, very important requirements leads to the development and observation of gradient flexoelectric deformations at very low DC voltage (Figure 2)9. According to the idea, originally developed by Prof. Derzhanski, the nonhomogeneity of the electric field is due to the accumulation of space charges, which are always present in the liquid crystal cell when one uses a DC voltage. The same effect was used by Derzhanski and Mitov10,11 to study experimentally the flexoelectrically textured MBBA nematic layer (Figure 4) and to calculate the total flexocoefficient (e1z+e3x) for the case of MBBA to be around 3·10-4 c.g.s. Let us mention that this measured value is near to that widely accepted in the literature, while for the sign of the total flexocoefficient there is no consensus. Later, the gradient flexoeffect was elaborated by Hinov and Vistin who have observed flexoelectric domains when the glass plates confining the liquid crystal were treated by soap (see below). Later the gradient flexoeffect was precised by Prost and Marcerou12 (Figure 3).
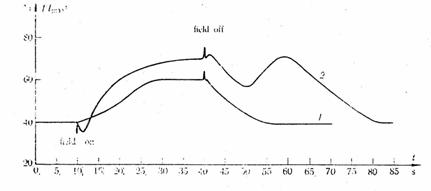Figure
2. Gradient
flexoelectric effect. The intensity of transmitted light as a function of
applied DC voltage.
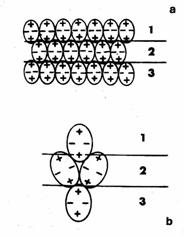
Figure 3. Quadrupoles and gradient flexoeffect.
Figure
4.
Flexoelectrically textured MBBA nematic layer.
Flexoeffect in a homogeneous electric field
The early study of the flexoeffect by the members of the Liquid Crystal Group was connected also with the study of the so-called polar flexoeffect, discovered for the first time by Helfrich13 and studied by Derzhanski and Hinov14 and by Derzhanski, Petrov and Mitov6. For example, the threshold transcedental equations for the polar voltage threshold have been solved analytically (some curves are shown in Figure 6).
Figure 5 Threshold voltage of polar
flexoelectric effect.
In reference 6 the polar flexoelectric deformations are a part of all possible one-dimensional flexoelectric deformations arising under the influence of a homogeneous electric field, regarded there. In effect, experimentally, the polar flexoeffect has been observed firstly by Petrov15 (see Figure 6). The concept of the gradient flexoeffect was elaborated by Hinov, Derzhanski and Mitov who regarded such an effect in non-planar geometry16. For the first time the authors have regarded the influence of low-frequency electric field on the flexoelectric deformations (similar results are presented in the Thesis of A. G. Petrov as well). The flexoelectric oscillations can be enhanced by simultaneous application of AC + DC electric fields3,17. Smultaneously with the study of the flexoelectric deformations, a significant part of the early study of the members of the Liquid Crystal Group have been devoted to the development of different methods for the determination of the flexoelectric coefficients18,19,20. Together with the study of the one-dimensional nonperiodic flexoelectric deformations, the authors investigating the flexoeffect, have also observed nearly-periodic flexoelectric deformations, which are along the initial orientation of the liquid crystal9,21. However, the easier study of the flexoelectric domains was possible after the treatment with soap of the glass plates confining the liquid crystal22,23. Another interesting flexoeffect – the creation of unidirectional spirals – was discovered in the large-pitch cholesterics24.
Figure
6 Polar flexoelectric effect. Observed
deformations.
Recently, the flexoelectric domains (flexo-dielectric walls) were studied more deeply and it was proved that they are created by the nonhomogeneity of the electric field due to the formation of the double electric layers for a DC voltage below 1V, or to unipolar (Figure 7) or bipolar injection, for the higher voltages (unpublished results). In addition, it was discovered that the flexoeffect changes the periodicity of the rubbing-induced domains, decreasing their period twice (Figure 7) (unpublished results). Furthermore, it was discovered that the use of electroactive materials such as hynhidron influences strongly the appearance and the kind of the flexoelectric domains (unpublished results).
Figure
7 Flexoelectric
domains (flexo-dielectric walls).
References:
1. R. Meyer, Phys. Rev. Lett.,
22(1969)918.
2. P. G. de Gennes, “Physics of Liquid Crystals”, Clarendon Press, Oxford
(1974).
3. A. I. Derzhanski and A. G. Petrov: “Flexoelectricity in nematic liquid
crystals”, Acta Physica Polonica A55(1979)747.
4. A. G. Petrov: “Measurements and interpretation of flexoelectricity” in
“Physical properties of Liquid Crystals: Nematics” emis. Data Reviews Series N
25, D. Dunmur, A. Fukuda and G. Luckhurst (eds), INSPEC (publ. IEE, London), pp
251-263 (2001).
5. C. Fan, Mol. Cryst. Liq. Cryst., 13 (1971)9.
6. A. Derzhanski, A. G. Petrov and M. D. Mitov, J. Phys. (Fr.), 39(1978)273.
7. A. Derzhanski and A. G. Petrov, in “Advances in Liquid Crystal Research and
Applications” (Pergamon, Oxford-Klado Budapest, 1980), vol. 1, p. 515.
8. S. A. Pikin: “Structural Transformations in Liquid Crystals”, Gordon and
Breach, New York (1991).
9. A. I. Derzhanski, A. G. Petrov, Chr. P. Khinov, and B. L. Markovski, Bulg. J.
Physics, 1(1974)165.
10. M. D. Mitov, Diploma Work: “Electrostructural Properties on Nematic Liquid
Cryastals”, Sofia University (1974).
11. A. Derzhanski and M. D. Mitov, C. R. Acad. Bulg. Sci. 28(1975)331.
12. J. Prost and J. Marcerou, J. Phys. (Fr.) 38(1977)315.
13. W. Helfrich, Appl. Phys. Lett., 24(1974)451.
14. A. I. Derzhanski and H. Hinov, J. Phys. (Fr.) 38(1977)1013.
15. A. G. Petrov, Thesis, Institute of Solid State Physics, Sofia (1974).
16. A. I. Derzhanski, H. P. Hinov and M. D. Mitov, Acta Phys. Pol. A55(1979)567.
17. A. G. Petrov, A. Derzhanski, K. Avramova and H. Hinov, Bulg. Patent Reg. N
40481 (1978).
18. A. I. Derzhanski and H. P. Hinov, Phys. Lett. A, 62(1977)36.
19. H. P. Hinov and A. I. Derzhanski, in “Advances in LC Research and
Applications”, L. Bata (ed.), Pergamon Press, Oxford-Akademiai Klado, Budapest
523 (1980).
20. H. P. Hinov and A. I. Derzhanski: in Liq. Cryst. Ord. Fl., 4 (1984)1103.
21. B. L. Markovski and A. G. Petrov, V Natl. Conf. Spectroscopy, Varna,
Bulgaria, Abstracts, p. 170 (1972).
22. H. Hinov, L. K. Vistin’ and Ju. G. Magakova, Kristallografiya, 23 (1978)583.
23. H. P. Hinov and L. K. Vistin’, J. Phys. (Fr.), 40 (1979)269.